 Raja Hannasa Fatika Effendy
Raja Hannasa Fatika Effendy
Apa Itu Kalkulus? Penjelasan Lengkap dan Aplikasinya
Edukasi | 2024-08-15 19:52:28Apa Itu Kalkulus? Penjelasan Lengkap dan Aplikasinya
Kalkulus, atau Calculus dalam bahasa Inggris, adalah bagian dari matematika yang fokus pada perubahan dan gerak. Ini meliputi turunan, integral, limit, dan fungsi. Kalkulus penting dalam banyak bidang, seperti fisika, teknik, dan ekonomi.
Kalkulus adalah penting untuk memahami perubahan di dunia nyata. Dengan kalkulus dasar, Anda bisa analisis dan prediksi berbagai proses dinamis. Ini membantu dalam berbagai bidang, dari fisika hingga ekonomi.
Contoh Kalkulus
Diferensiasi
Masalah Kecepatan: Misalkan posisi sebuah mobil pada waktu t dinyatakan dengan fungsi s(t) = t^2 + 2t. Turunan dari fungsi ini, s'(t) = 2t + 2, memberi tahu kita kecepatan mobil pada waktu t. Misalnya, pada waktu t = 3 detik, kecepatan mobil adalah s'(3) = 2(3) + 2 = 8 m/s.
 https://www.titoreista.com/ Materi Matematika Teknik" />
https://www.titoreista.com/ Materi Matematika Teknik" />Integrasi
Menghitung Area: Jika Anda memiliki fungsi f(x) = 3x dan ingin menghitung area di bawah kurva dari x = 0 hingga x = 2, Anda dapat menggunakan integrasi. Integral dari fungsi tersebut ∫ (dari 0 hingga 2) 3x dx akan memberikan area di bawah kurva. Hasilnya adalah ∫ (dari 0 hingga 2) 3x dx = 6 unit area.
Aplikasi dalam Fisika
Gerakan: Jika Anda tahu gaya F(t) yang bekerja pada sebuah benda sebagai fungsi waktu dan ingin mengetahui perubahan momentum benda, Anda bisa mengintegrasikan gaya tersebut. Jika F(t) = 4t, maka perubahan momentum selama waktu dari 0 hingga 3 detik adalah ∫ (dari 0 hingga 3) 4t dt = 18 kg·m/s.
Aplikasi dalam Ekonomi
Optimasi: Misalkan Anda memiliki fungsi biaya C(x) = x^2 - 6x + 8 yang menggambarkan biaya produksi x unit barang. Untuk menemukan jumlah barang yang meminimalkan biaya, Anda dapat menemukan turunan fungsi biaya, menyetarakannya dengan nol, dan memecahkan persamaan tersebut.
Kalkulus: Cabang Matematika yang Mempelajari Perubahan
Kalkulus adalah bagian dari matematika yang fokus pada perubahan dan gerakan. Ini sangat penting dalam ilmu pengetahuan dan teknologi saat ini. Definisi kalkulus adalah tentang analisis tak hingga dan matematika analitis.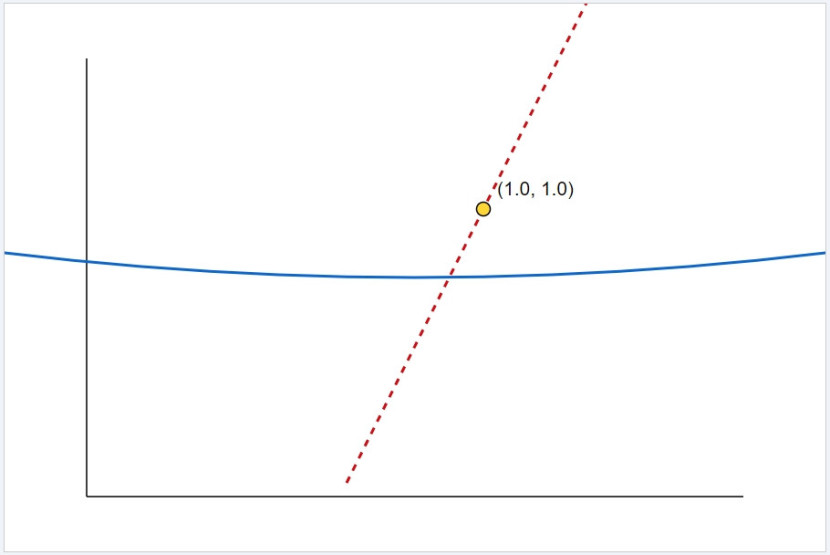
Definisi Kalkulus
Kalkulus mempelajari cara menghitung perubahan dan akumulasi. Istilah "kalkulus" berasal dari "calculus", yang berarti "batu kecil" untuk perhitungan. Ini melibatkan fungsi, limit, turunan, dan integral, penting untuk ilmu seperti fisika dan teknik.
Sejarah Perkembangan Kalkulus
Kalkulus berkembang di abad ke-17, dibantu oleh Isaac Newton dan Gottfried Leibniz. Mereka bekerja sendiri tetapi berkontribusi besar pada sejarah kalkulus. Perkembangan ini sangat penting dalam matematika modern.
Konsep Dasar Kalkulus
Kalkulus adalah bagian dari matematika yang fokus pada konsep penting seperti fungsi, limit, turunan, dan integral. Memahami konsep ini dengan baik sangat penting untuk menguasai analisis matematis yang lebih rumit.
Fungsi dan Limit
Fungsi adalah hubungan antara variabel-variabel, di mana perubahan pada satu variabel mempengaruhi yang lain. Konsep kalkulus sangat bergantung pada pemahaman fungsi. Limit adalah nilai yang dicapai oleh fungsi saat variabel mendekati nilai tertentu. Memahami limit membantu kita analisis fungsi dan menemukan nilai yang tidak terdefinisi.
Turunan dan Integral
Turunan mengukur laju perubahan fungsi terhadap variabelnya. Ini membantu kita menghitung kecepatan perubahan, gradien, dan mengoptimalkan fungsi. Integral adalah lawan dari turunan, digunakan untuk menentukan luas daerah di bawah kurva. Ini penting dalam analisis matematis, seperti prediksi perubahan volume dan jarak.
Memahami konsep kalkulus, termasuk fungsi, limit, turunan, dan integral, adalah kunci untuk menguasai analisis matematis yang lebih kompleks.
Apa Itu Kalkulus?
Kalkulus adalah bagian dari matematika yang fokus pada perubahan dan gerakan. Ini meliputi turunan, integral, limit, dan fungsi. Kalkulus penting dalam banyak bidang, seperti fisika, teknik, dan ekonomi.
Kalkulus bisa dilihat sebagai bagian matematika yang mempelajari perubahan dan gerakan. Ini membantu kita menghitung laju dan akumulasi perubahan.
Kalkulus sangat penting dalam berbagai bidang. Dari analisis populasi hingga desain mesin, kalkulus sangat berguna. Ini membantu kita menyelesaikan masalah dengan lebih baik.
Ringkasnya, kalkulus adalah bagian matematika yang khusus untuk perubahan dan gerakan. Dengan konsep seperti turunan dan integral, kalkulus sangat berguna dalam banyak bidang.
Cabang-Cabang Kalkulus
Kalkulus adalah bagian dari matematika yang fokus pada perubahan. Ada dua bagian utama: kalkulus diferensial dan kalkulus integral. Kedua bagian ini penting dalam banyak bidang, seperti sains, teknik, dan ekonomi.
Kalkulus Diferensial
Kalkulus diferensial mempelajari turunan. Ini membantu kita mengerti perubahan dan bagaimana mencapai nilai maksimum atau minimum. Contohnya, kita bisa hitung kecepatan atau percepatan.
Kalkulus Integral
Kalkulus integral fokus pada luas daerah atau volume benda. Ini berguna untuk menghitung jarak, energi, dan lain-lain. Keduanya, integral dan diferensial, sering digunakan bersama.
Keduanya, kalkulus diferensial dan kalkulus integral, sangat penting. Mereka membantu kita memahami fenomena dalam matematika lanjut dan bidang terkait.
Aplikasi Kalkulus dalam Kehidupan Sehari-hari
Kalkulus seringkali tidak terlihat, tapi penting dalam kehidupan kita. Matematika praktis ini berguna tidak hanya di sekolah, tapi juga di berbagai aspek kehidupan.
Contohnya, kalkulus digunakan untuk menghitung laju pertumbuhan. Ahli menggunakan kalkulus untuk memprediksi pertumbuhan populasi hewan atau tumbuhan. Ini membantu dalam konservasi alam.
Kalkulus juga penting dalam menghitung laju perubahan harga. Ekonom dan bisnis memakai kalkulus untuk mengerti tren pasar. Mereka juga membuat keputusan investasi dan strategi pemasaran yang lebih baik.
Dalam bidang cuaca, kalkulus sangat penting. Meteorolog memakai kalkulus untuk memodelkan pola cuaca. Mereka juga membuat prakiraan cuaca yang lebih akurat.
Jadi, kalkulus bukan hanya soal matematika tingkat lanjut. Ia punya banyak penerapan yang bermanfaat dalam kehidupan kita sehari-hari.
Penerapan Kalkulus dalam Bidang Sains dan Teknologi
Kalkulus, bagian dari matematika yang fokus pada perubahan, sangat penting dalam sains dan teknologi. Ini digunakan di fisika, teknik, dan ekonomi.
Fisika
Penerapan kalkulus dalam fisika meliputi mekanika, termodinamika, dan listrik. Kalkulus diferensial membantu analisis pergerakan dan kecepatan. Kalkulus integral digunakan untuk menghitung volume dan energi.
Teknik
Terapan kalkulus dalam teknik penting untuk desain struktur dan kontrol sistem. Ini membantu analisis fenomena seperti regangan dan aliran fluida. Ini memungkinkan teknologi yang lebih efisien.
Ekonomi
Aplikasi kalkulus dalam ekonomi membantu optimalkan proses dan analisis pasar. Kalkulus diferensial untuk titik optimal, dan kalkulus integral untuk tren ekonomi.
Kalkulus sangat penting dalam berbagai bidang ilmu. Memahami kalkulus membantu inovasi dan solusi dalam sains dan teknologi.
Tokoh-Tokoh Penting dalam Perkembangan Kalkulus
Kalkulus adalah cabang matematika yang mempelajari perubahan. Dua tokoh penting dalam perkembangannya adalah Isaac Newton dan Gottfried Leibniz. Mereka berkontribusi besar dalam perkembangan kalkulus pada abad ke-17.
Isaac Newton, seorang fisikawan dan matematikawan Inggris, dikenal dengan teori kalkulus diferensialnya. Ia mengembangkan konsep seperti turunan, limit, dan integral. Konsep-konsep ini membantu memahami perubahan dan pergerakan di alam semesta.
Newton juga memanfaatkan kalkulus dalam penyelidikannya tentang hukum gravitasi dan mekanika klasik.
Gottfried Leibniz, seorang matematikawan Jerman, mengembangkan notasi dan konsep kalkulus integral. Ia memperkenalkan simbol-simbol matematika yang kini umum digunakan, seperti symbol integral (∫) dan simbol turunan (d/dx). Kontribusi Leibniz penting dalam mempermudah pemahaman dan aplikasi kalkulus.
Newton dan Leibniz mengembangkan kalkulus secara terpisah. Namun, kontribusi mereka besar dalam perkembangan matematika analitis. Mereka membuka jalan bagi ilmuwan lain untuk terus mengeksplorasi dan mengaplikasikan kalkulus.
Metode Pembelajaran Kalkulus yang Efektif
Belajar kalkulus efektif butuh dua cara utama: praktik soal dan paham konsep dasar. Gabungkan latihan intensif dengan paham konseptual, biar kemampuan belajar kalkulus siswa naik.
Praktik Soal
Latihan soal adalah kunci utama untuk menguasai kalkulus. Dengan latihan, siswa bisa kembangkan keterampilan komputasi dan pemecahan masalah. Ini juga bikin mereka paham metode pembelajaran kalkulus lebih dalam.
- Mulai dari soal sederhana, lalu tingkatkan kompleksitasnya.
- Terapkan konsep baru dalam soal-soal.
- Gunakan sumber online, seperti video dan bank soal, untuk latihan.
Belajar Konsep Dasar
Latihan soal itu penting, tapi paham konsep dasar kalkulus juga krusial. Konsep seperti fungsi, limit, turunan, dan integral adalah dasar. Mereka penting untuk maju dalam belajar kalkulus.
- Pahami definisi dan sifat konsep dasar kalkulus.
- Cari contoh aplikasi konsep dasar di kehidupan sehari-hari.
- Hubungkan konsep dasar untuk pemahaman yang lebih luas tentang konsep dasar kalkulus.
Dengan gabungkan praktik soal dan paham konsep dasar, siswa bisa belajar kalkulus dengan baik. Mereka akan paham lebih dalam.
Kalkulus dan Matematika Lanjutan
Kalkulus adalah dasar penting dalam matematika lanjutan. Memahami konsep dasar kalkulus membuat kita mudah belajar matematika yang lebih kompleks. Contohnya, analisis matematis, persamaan diferensial, dan geometri analitik.
Memahami perubahan dan menghitung laju perubahan melalui kalkulus sangat berguna. Ini membantu kita dalam matematika lanjutan dan kalkulus lanjut. Kita bisa lebih baik memahami fenomena matematis kompleks.
Contoh aplikasi matematika analitik yang menggunakan kalkulus antara lain:
- Analisis vektor dan tensor
- Teori ukuran dan fungsi analitik
- Persamaan diferensial parsial
- Topologi dan geometri diferensial
Dengan menguasai kalkulus, kita siap menjelajahi matematika lanjutan. Ini memberikan wawasan dan pemahaman lebih dalam tentang fenomena alam dan sistem kompleks.
Buku-Buku Kalkulus Terbaik untuk Pemula
Mempelajari kalkulus sebagai pemula bisa terasa sulit. Namun, dengan buku yang tepat, belajar jadi lebih mudah dan menyenangkan. Berikut ini adalah beberapa buku kalkulus terbaik untuk kalkulus pemula:
- "Kalkulus untuk Pemula" karya Howard Anton - Buku ini menjelaskan konsep dasar kalkulus dengan cara yang mudah dipahami. Ada banyak contoh dan latihan soal.
- "Kalkulus" karya James Stewart - Buku ini adalah referensi utama untuk banyak mahasiswa. Menyajikan konsep pengantar kalkulus dengan cara yang sistematis dan komprehensif.
- "Pemahaman Kalkulus Dasar" karya Michael Spivak - Buku ini fokus pada pemahaman konseptual. Cocok untuk kalkulus pemula yang ingin membangun pondasi yang kuat.
Buku-buku ini menjelaskan pelajaran kalkulus dengan cara yang sistematis. Penjelasannya jelas dan dilengkapi dengan contoh aplikasi yang relevan. Bagi Anda yang baru memulai, ketiga buku ini bisa membantu memahami konsep dasar dan meningkatkan kemampuan menyelesaikan soal-soal kalkulus pemula.
Manfaat Mempelajari Kalkulus
Mempelajari kalkulus bukan hanya menantang intelektual. Ia juga memberikan banyak manfaat dalam kehidupan sehari-hari. Berikut ini beberapa alasan mengapa kalkulus sangat berharga:
- Memahami Fenomena Perubahan dan Pergerakan: Kalkulus membantu kita memahami perubahan dan pergerakan di berbagai bidang. Ini termasuk fisika, teknik, dan ekonomi.
- Menerapkan Konsep Kalkulus dalam Berbagai Bidang: Memahami kalkulus membuka pintu untuk aplikasi konsepnya di berbagai bidang. Ini membantu dalam mengambil keputusan yang lebih baik.
- Mengembangkan Kemampuan Berpikir Analitis dan Pemecahan Masalah: Belajar kalkulus melatih kemampuan berpikir analitis dan pemecahan masalah. Keterampilan ini sangat berguna dalam berbagai aspek kehidupan.
- Memperoleh Landasan Kuat untuk Mempelajari Matematika Lanjutan: Penguasaan kalkulus memberikan fondasi kuat untuk mempelajari matematika lanjutan. Ini termasuk aljabar linier, analisis real, dan persamaan differensial.
Dengan memahami dan menerapkan konsep kalkulus, kita bisa meningkatkan kemampuan matematika praktis. Ini membantu dalam berbagai aspek kehidupan. Mempelajari kalkulus adalah investasi berharga untuk karier dan pengembangan diri.
Disclaimer
Retizen adalah Blog Republika Netizen untuk menyampaikan gagasan, informasi, dan pemikiran terkait berbagai hal. Semua pengisi Blog Retizen atau Retizener bertanggung jawab penuh atas isi, foto, gambar, video, dan grafik yang dibuat dan dipublished di Blog Retizen. Retizener dalam menulis konten harus memenuhi kaidah dan hukum yang berlaku (UU Pers, UU ITE, dan KUHP). Konten yang ditulis juga harus memenuhi prinsip Jurnalistik meliputi faktual, valid, verifikasi, cek dan ricek serta kredibel.











