Wanda Ningsih

Subring dan Suatu Ring di Dalam Ring

Eduaksi | 2022-05-18 03:00:30

Subring dan Suatu Ring Di Dalam Ring

ABSTRAK

Dalam teori ring, salah satu contoh ring yang sudah umum diketahui adalah himpunan semua bilangan bulat {Z} terhadap operasi penjumlahahan dan perkalian. Beberapa sub himpunan tak kosong yang dimiliki himpunan {Z} beberapa diantaranya adalah himpunan 2{Z} (himpunan semua bilangan genap) dan himpunan 2{Z}+1 (himpunan semua bilangan ganjil).

Diperhatikan bahwa himpunan 2{Z} merupakan ring terhadap operasi penjumlahan dan perkalian. Di lain pihak, himpunan 2{Z}+1 bukan merupakan ring terhadap operasi penjumlahan dan perkalian dikarenakan operasi penjumlahan tidak tertutup pada himpunan 2{Z}+1 (jumlahan dua bilangan ganjil hasilnya bukan bilangan ganjil). Dengan memperhatikan dua fenomena tersebut, suatu subhimpunan tak kosong dari sutau ring bisa merupakan ring atau tidak terhadap operasi yang sama pada ringnya. Pada kasus subhimpunan tak kosong tersebut merupakan ring, memotifasi adanya definisi dari subring.

kata kunci : subring dan ring

Definisi 1.

Misalkan S adalah himpunan bagian tak kosong dari di dalam ring (R,+, .). Himpunan S disebut subring dari R jika S merupakan subring terhadap operasi yang sama pada S, yaitu operasi penjumlahan + dan perkalian . (cdot).

Contoh 2.

Berikut adalah contoh-contoh subgrup.

1.Mudah dipahami bahwa 2\Z merupakan subring dari ring (Z,+, .). Secara umum, untuk setiap

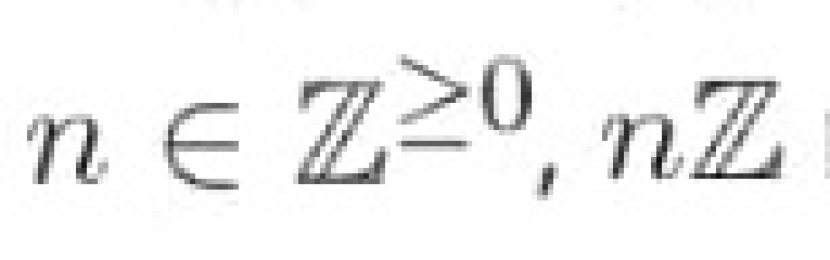
2.Karena (Z,+, .) dan (R,+,.) keduanya merupakan ring dan Z subset R, maka Z merupakan subring dari ring R.

3.Himpunan semua matriks diagonal berukuran 2X2, yaitu

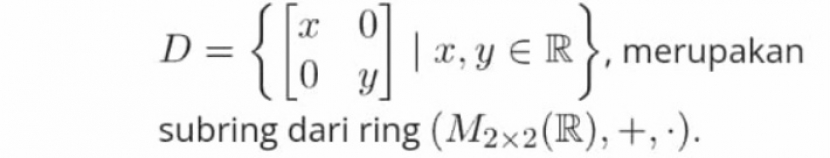
4.Setiap ring (R,+,\cdot) selalu memuat subring, yaitu paling tidak memuat subring {0R} dan subring R. Kedua subgrup itu disebut subring trivial.

Untuk membuktikan suatu sub himpunan tak kosong dari suatu ring merupakan subring, perlu menyelidiki syarat-syarat supaya sub himpunan tersebut menjadi ring.Jika diperhatikan lebih seksama, syarat berlakunya sifat assositaif, distributif, bisa kita abaikan karena sudah terwarisi dari sifat ringnya. Disamping itu, jika ditinjau dari operasi penjumlahannya, suatu subhimpunan merupakan subring maka terhadap operasi penjumlahan subhimpunan tersebut merupakan subgrup. Dengan adanya fakta ini, diperoleh Teorema berikut ini.

Teorema 3.

Misalkan (R,+ .) merupakan ring dan S adalah suatu himpunan tak kosong dari R. Himpunan S merupakan subring dari R jika dan hanya jika pada S memenuhi sifat berikut:

Berikut ini adalah contoh penggunaan teorema syarat perlu dan cukup untuk subring.

Contoh 4. Diketahui bahwa himpunan M2x2(R) merupakan ring terhadap operasi penjumlahan dan perkalian matriks. Buktikan bahwa himpunan matriks segitiga atas

Bukti.

1.Perhatikan bahwa bukti

Berdasarkan syarat perlu dan cukup subring diperoleh bahwa himpunan TA2x2(R) merupakan subring dari M2x2(R)

Daftar Pustaka

https://strukturaljabar.mipa.ugm.ac.id/subring-suatu-ring-di-dalam-ring/