Mengenal Sistem Persamaan Linear Dua Variabel dengan Metode Eliminasi Gauss Jordan

Pendidikan dan Literasi | 2023-12-11 00:14:11

Persamaan linear adalah persamaan aljabar yang tiap sukunya mengandung konstanta atau perkalian konstanta dengan variabel tunggal, dan pangkat tertinggi dari variabelnya selalu satu. Persamaan ini disebut linear karena hubungan matematis ini dapat digambarkan sebagai garis lurus dalam sistem koordinat Kartesius.

PENGERTIAN SISTEM PERSAMAAN LINEAR DUA VARIABEL DAN GAUSS JORDAN

Sistem persamaan linear dua variabel atau biasa disingkat dengan SPLDV merupakan sistem persamaan linear yang terdiri dari dua persamaan linear dan memiliki dua variabel, misalkan X dan Y, serta memiliki bentuk umum ax + by = c. SPLDV biasanya digunakan untuk menyelesaikan masalah sehari – hari yang membutuhkan penggunaan seperti menentukan harga suatu barang dan masih banyak yang lainnya.

Materi terkait sistem SPLDV biasanya dijumpai pada saat SMP dan SMA/SMK sederajat, dengan penyelesaian dapat dilakukan dengan berbagai cara atau metode, seperti metode eliminasi, metode substitusi, metode gabungan dan metode grafik. Kali ini kita akan membahas sistem persamaan linear dua variabel dengan metode eliminasi Gauss Jordan yang akan dijumpai di dunia perkuliahan.

Apa itu eliminasi Gauss Jordan? Yuk Simak penjelasan berikut

Metode Gauss-Jordan adalah sebuah metode dalam aljabar linear yang digunakan untuk menyelesaikan sistem persamaan linear dengan mengubah matriks koefisien menjadi bentuk matriks eselon baris tereduksi. Metode ini melibatkan prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks eselon baris tereduksi dengan metode operasi baris elementer. Eliminasi Gauss-Jordan adalah modifikasi dari metode eliminasi Gauss, yang dijelaskan oleh Jordan di tahun 1887. Dalam eliminasi Gauss-Jordan, matriks A dieliminasi menjadi matriks identitas I, dan solusinya langsung diperoleh dari vektor kolom b hasil proses eliminasi.

Cara Penyelesaian dari SPLDV menggunakan metode Gauss Jordan:

 

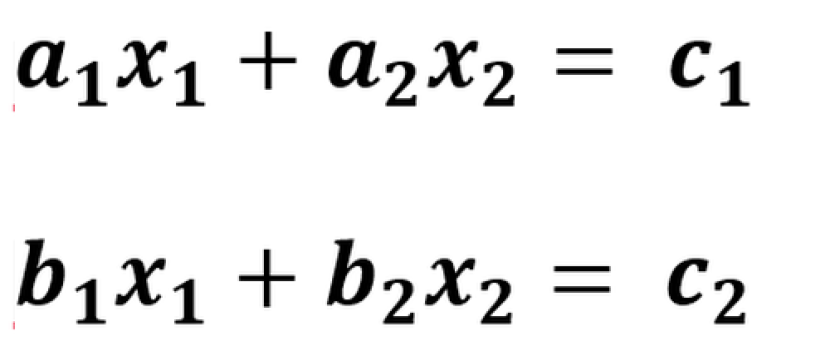
• Langkah yang pertama merubah persamaan tersebut kedalam bentuk matriks

 

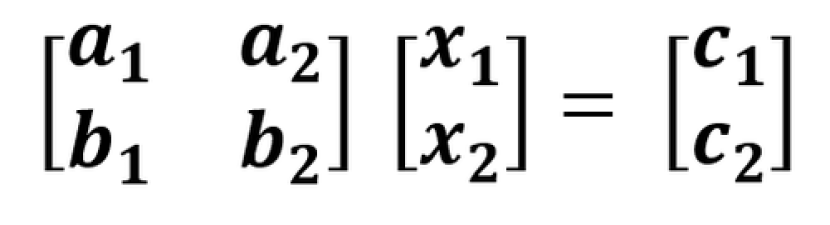
• Langkah kedua mengubah matriks tersebut dalam bentuk Operasi Baris Elementer (OBE)

 

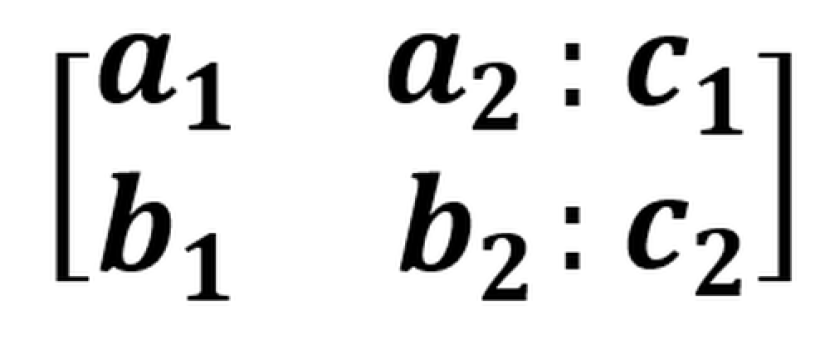
• Langkah ketiga buatlah bentuk OBE menjadi bentuk identitas seperti dibawah ini, dengan cara eleminasi:

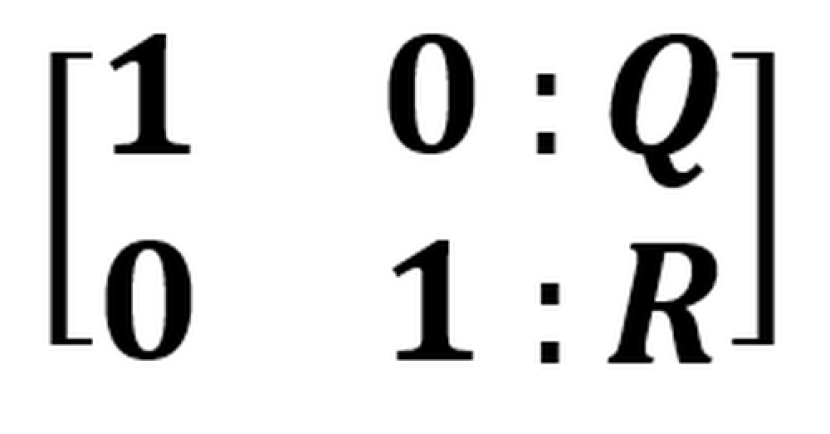
Akan didapatkan hasilnya yaitu:

Contoh soal penyelesaian sistem persamaan linear dua variabel dengan metode Gauss Jordan

Tentukan himpunan dari penyelesaian dan dari persamaan berikut ini

kita asumsikan untuk persamaan pertama sebagai R1 dan persamaan kedua sebagai R2.

 

• Pada eliminasi yang pertama kita akan merubah persamaan kedua yaitu angka 3 menjadi angka 0 dengan mengeliminasi 3R1 dan R2

 

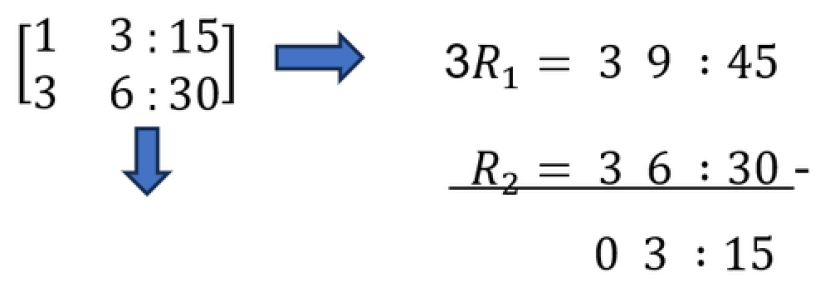
• Eliminasi kedua merubah persamaan kedua yaitu angka 3 menjadi angka 1 dengan membagi1/3 dari persamaan kedua.

 

• Eleminasi ketiga merubah persamaan pertama yaitu angka 3 menjadi angka 0 dengan mengeliminasi

Jadi, dapat di lihat dari gambar diatas yaitu hasil penyelesaian dari persamaan linear dua variabel adalah X1= 0 dan X2= 5.